cs61a: function
主要来自lec以及教材
入门
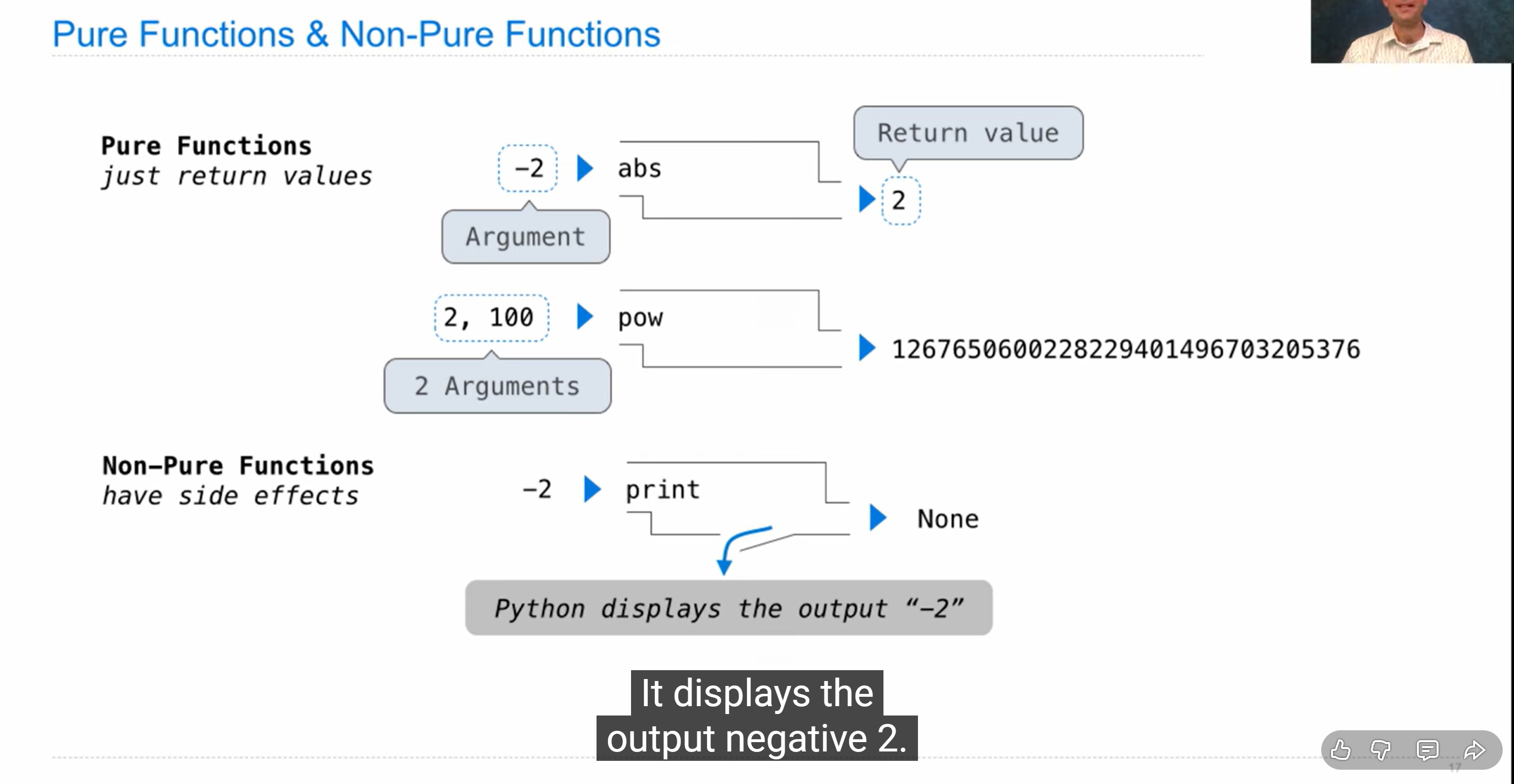
函数分为pure function 与 none-pure function:
优秀的函数思想,函数即抽象: - 每个函数应该只做一件事。这项工作应该能用一个简短的名称来概括,并能用一行文字描述其特征。如果一个函数按顺序执行多项任务,则应将其拆分为多个函数 - 不要重复自己(Don't Repeat Yourself)。这是软件工程的一个核心信条。所谓的 DRY 原则指出,多段代码不应描述冗余的逻辑。相反,逻辑应该只实现一次,赋予其名称,然后多次应用。如果你发现自己在复制粘贴一段代码,那么你可能已经找到了一个进行函数抽象的机会 - 函数的定义应具有通用性。比如,作为 pow 函数的一个特例,平方函数就不在 Python 库中,因为 pow 函数可以计算任意幂次。
一个对象(object)无缝地将数据和操纵该数据的逻辑捆绑在一起。
将名称与值绑定,之后通过名称检索可能的值,意味着解释器必须维护某种内存来跟踪记录名称、值和绑定关系,这种内存被称为环境(environment)。函数内先在函数的 frame(帧)里找变量,找不到再到global frame里找.
frame(帧) & scope(作用域)
x = 10
def f(y):
z = y + x
return z
f(5)
对于多重赋值,所有 = 右边的表达式都会先求值,然后再与左边的名称绑定。比如:
a = 10
b = 5
a, b = b, a+b
在python中变量可与函数绑定,比如定义了函数
xxx()后可以f=xxx,以后就可以f()等效于xxx()。
文档字符串(docstring)应当在定义函数时与函数一起缩进,用三个引号括起来,在help(<function name>)时就会输出,注释则不会,例如:
>>> def pressure(v, t, n=6.022e23):
"""计算理想气体的压力(单位:帕斯卡)
使用理想气体定律:http://en.wikipedia.org/wiki/Ideal_gas_law
v -- 气体体积,单位:立方米
t -- 绝对温度,单位:开尔文
n -- 气体粒子数
>>> a = pressure(10,21)
xx
>>> b = ...
yy
"""
k = 1.38e-23 # 玻尔兹曼常数
return n * k * t / v
n=...这里没有进行赋值操作而是表示调用pressure函数时使用的默认值,而"""之间的>>> ...起测试作用。注意,help(xx)在使用之前需要保证解释器读取得到这个函数,比如xx在hw01文件夹下的某个python文件内,在这个文件夹内打开解释器,那么要先import hw01让解释器的环境里存在hw01,之后再执行help(hw01.xx).
运行与测试
-
python3 lab00.py -
-i:-i选项会先运行文件中的代码,然后打开一个交互式Python会话 (显示 >>> 提示符)。 你可以执行表达式,比如调用你定义的函数。 -
-m doctest: 运行文件中的doctest。 Doctest是函数文档字符串里的示例代码。文件中的每个测试都包含>>>,后跟一些 Python 代码和预期输出。如果所有doctest都通过,不会有任何输出。 否则会显示测试失败的信息。
and与or的短路
短路之后不一定输出True/False,而是输出最后计算出的东西,比如True and 3会输出3,False and 0则输出False,而1 and 1 > 0会输出True
高阶函数
我们最初引入用户自定义函数,是为了把数值运算的模式抽象出来,使其不再依赖于具体的数字;而当我们引入高阶函数后,开始出现一种更强大的抽象形式:有些函数表达的是通用的计算方法,与它们具体调用的函数无关。
从不同求和(自然数,平方,有规律的式子)的函数写法中可以发现强烈的相似性,代码中经常会出现一些反复使用的编程模式或底层逻辑,只是每次配合使用的具体函数不同。,于是可以抽象出把函数作为参数的高阶函数:
>>> def summation(n, term):
total, k = 0, 1
while k <= n:
total, k = total + term(k), k + 1
return total
>>> def identity(x):
return x
>>> def sum_naturals(n):
return summation(n, identity)
>>> sum_naturals(10)
55
关于抽象
用户自定义函数是一种至关重要的抽象机制,因为它们让我们能把通用的计算方法作为编程语言中的显式元素表达出来。现在我们又看到,高阶函数允许我们操作这些通用方法,从而创造更进一步的抽象。A new level of abstraction,应该时刻留意程序中潜在的底层抽象,基于它们进行构建,并泛化出更强大的抽象。这并不是说永远要用最抽象的方式写程序——高手知道如何选择与任务相匹配的抽象层次。但重要的是,我们要能用这些抽象去思考,这样在新的场景中才能迅速应用它们。高阶函数的意义在于,它们让我们能把这些抽象显式地表示为编程语言中的元素,像对待其他计算元素一样去操作它们。
一等地位
一般来说,编程语言会对计算元素的操作方式施加各种限制。限制最少的元素被称为具有一等地位(first-class status)。一等元素通常享有以下“权利和特权”:
- 可以绑定到名字
- 可以作为参数传递给函数
- 可以作为函数的结果返回
- 可以出现在数据结构中
Python 授予函数完整的一等地位,由此带来的表达能力提升是巨大的。
柯里化
给定一个函数 f(x, y),我们可以定义一个函数 g 使得 g(x)(y) 等价于 f(x, y)。这里 g 是一个高阶函数,它接受单个参数 x 并返回另一个接受单个参数 y 的函数。这种转换就称为柯里化(curring):
>>> def curried_pow(x):
def h(y):
return pow(x, y)
return h
>>> curried_pow(2)(3)
8
Lambda表达式
有的过程函数没必要取名,可以使用 lambda 表达式实时创建函数(匿名函数)。lambda 表达式求值后得到一个函数,这个函数的函数体只有一个返回表达式,不允许出现赋值或控制语句:
def compose1(f, g):
return lambda x: f(g(x))
f = compose1(lambda x: x * x,
lambda y: y + 1)
result = f(12)
>>> result
169
相当于直接提出 lambda x: x的函数具体内容。
(lambda: 3)()输出3.
装饰器
>>> def trace(fn):
def wrapped(x):
print('-> ', fn, '(', x, ')')
return fn(x)
return wrapped
>>> @trace
def triple(x):
return 3 * x
>>> triple(12)
-> <function triple at 0x102a39848> ( 12 )
36
>>> def triple(x):
return 3 * x
>>> triple = trace(triple)
补充
当我们希望编写一个接受任意数量参数的函数,然后使用完全相同的参数调用另一个函数: 与其列出函数的正式参数,不如使用 *args,它表示传递给函数的所有参数。 然后,我们可以将 *args 传递给另一个函数,从而使用相同的参数调用该函数。 例如:
>>> def printed(f):
... def print_and_return(*args):
... result = f(*args)
... print('Result:', result)
... return result
... return print_and_return
>>> printed_pow = printed(pow)
>>> printed_pow(2, 8)
Result: 256
256
>>> printed_abs = printed(abs)
>>> printed_abs(-10)
Result: 10
10
做hw2时有个很有趣的事:
def make_repeater(f, n):
def xx(num):
mark = n
while mark != 0:
num, mark = f(num), mark-1
return num
return xx
def make_repeater(f, n):
def xx(num):
while n != 0:
num, n = num + f(num), n-1
return num
return xx
def make_repeater(f, n):
def xx(num):
nonlocal n
while n != 0:
num, n = f(num), n - 1
return num
return xx
递归函数
互递归:两个函数相互调用
本质:把问题不断化简为同类更简单情况,直到出现基本问题